A widely used industrial flow meter is the Venturi. The practical design was patented by Clemens Herschell in 1895, whilst crediting Giovanni Battista Venturi for the idea of measuring flow rate by looking at the difference in pressure across a restriction made of two truncated cones joined together at their narrow ends.

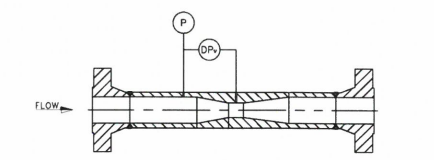
Figure 1 - Venturi
This simple device is the application of the principle that Daniel Bernouilli had published in 1738; that for a theoretical fluid with no viscosity ("inviscid"), an increase in the flow velocity occurs simultaneously with a decrease in the pressure. Combining this with the continuity equation provides a relation between the flow rate through a restriction device such as the Venturi and the resulting differential pressure (written as either DP or ∆P) between the inlet and the throat:
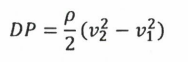
where ρ is the fluid density, 𝜈1, the fluid velocity at the inlet and 𝜈2 the velocity at the throat of the Venturi. This equation therefore equates the gain in kinetic energy to the pressure energy lost by the fluid, assuming no other energy exchange of energy takes place (e.g. no friction in the fluid, or heat lost from the system).
As mass is conserved through the Venturi, such that:

Then by combining these two (setting D as the pipe diameter at the inlet [point 1], and d as the throat diameter [point 2], where 𝛽 = d / D for a Venturi) we can find the mass flow rate:
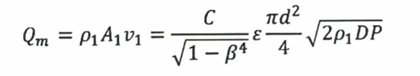
This is the fundamental equation for differential pressure metering, relating the measured DP to the mass flow rate passing through a restriction device of known size, at the given density conditions.
The theoretical derivation of this equation would exclude two parameters given in the equation above: the discharge coefficient, C, is included to make allowance for the flow being non-ideal, and therefore takes account of viscous effects; the expansibility, ɛ, allows for the difference in the fluid density between the inlet and the throat for compressible fluids, and can be calculated for a gas passing through a Venturi (although beyond the scope of this article).
For a Venturi, both parameters typically have a value close to 1.0; for more information, industry generally refers to ISO 5167-4:2003 (For other metering devices that produce a differential pressure, such as an orifice plate, nozzle, or cone, the discharge coefficient is typically significantly lower than a Venturi. The expansibility factor also cannot be theoretically calculated, but instead a "general" equation for a given range of physically similar devices can be found by collating the results of many relevant flow tests, such as those given in other parts of ISO 5167.).
Wet gas metering is challenging, as the generalisations of single phase (gas or liquid only) flow are no longer applicable. An additional wet gas correction (WGC) term needs to be applied to correct the gas flow rate for the presence of liquid, which would otherwise cause it to be too high (to "over-read").

This equation states that to calculate the true gas mass flow rate (Qmg) it is necessary to take the indicated mass flow rate (Qmgi - which is generally Qm from the previous equation, but where the density at the inlet is the gas density) and divide it by a correction factor.
